Ondas

Ondas

Em física, uma onda é uma perturbação oscilante de alguma grandeza física no espaço e periódica no tempo. A oscilação espacial é caracterizada pelo comprimento da onda e o tempo decorrido para uma oscilação é medido pelo período da onda, que é o inverso da sua frequência. Estas duas grandezas estão relacionadas pela velocidade de propagação da onda.

Fisicamente, uma onda é um pulso energético que se propaga através do espaço ou através de um meio (líquido, sólido ou gasoso), com velocidade definida. Segundo alguns estudiosos e até agora observado, nada impede que uma onda magnética se propague no vácuo ou através da matéria, como é o caso das ondas eletromagnéticas no vácuo ou dos neutrinos através da matéria, onde as partículas do meio oscilam à volta de um ponto médio mas não se deslocam. Exceto pela radiação eletromagnética, e provavelmente as ondas gravitacionais, que podem se propagar através do vácuo, as ondas existem em um meio cuja deformação é capaz de produzir forças de restauração através das quais elas viajam e podem transferir energia de um lugar para outro sem que qualquer das partículas do meio seja deslocada; isto é, a onda não transporta matéria. Há, entretanto, oscilações sempre associadas ao meio de propagação.

Uma onda pode ser longitudinal quando a oscilação ocorre na direção da propagação, ou transversal quando a oscilação ocorre na direção perpendicular à direção de propagação da onda.

                                        Meios de Propagação

Podemos classificar os meios onde as ondas se podem propagar das seguintes formas :

• Meios lineares: se diferentes ondas de qualquer ponto particular do meio em questão podem ser somadas;
• Meios limitados: se ele é finito em extensão, caso contrário são considerados ilimitados;
• Meios uniformes: se suas propriedades físicas não podem ser modificadas de diferentes pontos;
• Meios isotrópicos: se suas propriedades físicas são as mesmas em quaisquer direções.

                                   Ondas Transversais e Longitudinais

Ondas transversais são aquelas em que a vibração é perpendicular à direção de propagação da onda; exemplos incluem ondas em uma corda e ondas eletromagnéticas.

Ondas longitudinais são aquelas em que a vibração ocorre na mesma direção do movimento; um exemplo são as ondas sonoras.

                                  Descrição de Uma Onda Pela Física

Ondas podem ser descritas usando um número de variáveis, incluindo: frequência, largura e altura da onda, amplitude e período.

A amplitude de uma onda é a medida da magnitude de um distúrbio em um meio durante um ciclo de onda. Por exemplo, ondas em uma corda têm sua amplitude expressada como uma distância (metros), ondas de som como pressão (pascals) e ondas eletromagnéticas como a amplitude de um campo elétrico (volts por metro). A amplitude pode ser constante (neste caso a onda é uma onda contínua), ou pode variar com tempo e/ou posição. A forma desta variação é o envelope da onda.

O período é o tempo(T) de um ciclo completo de uma oscilação de uma onda. A frequência (F) é período dividido por uma unidade de tempo (exemplo: um segundo), e é expressa em hertz. Veja abaixo:

.

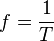Quando ondas são expressas matematicamente, a frequência angular (ômega; radianos por segundo) é constantemente usada, relacionada com frequência f em:

.

            

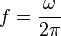                                   Ondas Estacionárias e Ondas Não-Estacionárias

Ondas que permanecem no mesmo lugar são chamadas ondas paranticas, como as vibrações em uma corda de violino.

Corda a vibrar na frequência fundamental e no 2º, 3º, 4º, 5º, e 6º harmónicos.

Quando uma corda é deformada, a perturbação propaga-se por toda a corda, reflectindo-se nas suas extremidades fixas. Da interferência das várias ondas pode resultar uma onda estacionária, ou seja, uma oscilação que aparenta não se mover através do material. Os nodos resultam da interferência (destrutiva) entre a crista e o ventre de duas ondas. Nos anti-nodos, onde o deslocamento é máximo, a interferência dá-se entre duas cristas ou dois ventres de onda. Cada padrão de oscilação corresponde a uma determinada frequência a que se chama um harmónico. As frequências de vibração variam com o comprimento da corda e com as suas características (material, tensão, espessura), que determinam a velocidade de propagação das ondas. À frequência mais baixa a que a corda vibra chama-se frequência fundamental.

Ondas que se movem (não-estacionárias) têm uma perturbação que varia tanto com o tempo t quanto com a distância z e pode ser expressada matematicamente como: , onde A(z,t) é o envelope de amplitude da onda, k é o número de onda e φ é a constante de base. A velocidade v desta onda é dada por: , onde λ é o comprimento de onda.

                             A Equação Universal Da Onda

A forma mais simples desta equação é:

Em que:

• v: Velocidade da onda
• λ: Comprimento de onda
• f: Frequência de onda

Y = A.sen[2.π(t/T - x/λ) + φ]

                            Exercícios Resolvidos

01. Uma onda periódica é produzida numa corda tensa mediante uma fonte vibratória de freqüência 2,0 Hz. Sabendo-se que o comprimento das ondas produzidas é 10 cm, podemos afirmar que a velocidade de propagação dessas ondas é:

a) 5,0 cm/s
b) 8,0 cm/s
c) 10 cm/s
d) 12 cm/s
e) 20 cm/s
Resolução

v = 10 · 2
v = 20 cm/s

Resposta: E

02. O gráfico abaixo representa uma onda que se propaga com velocidade igual a 300m/s.

Determine:

a) a amplitude da onda

b)o comprimento da onda

c) a frequência

Resolução:

a)

A Amplitude da onda é dada pela distância da origem até a crista da onda, ou seja:

b)

O comprimento de onda é dado pela distância entre duas cristas ou entre 3 nodos, ou seja:

Como a figura mostra a medida de três “meios-comprimento de onda”, podemos calculá-lo:

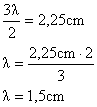
c)

Sabendo a velocidade de propagação e o comprimento de onda, podemos calcular a frequência através da equação:

Substituindo os valores na equação:

03. A mão da pessoa, segurando a extremidade de uma corda tensa e flexível, produz uma perturbação que se propaga ao longo da corda. A perturbação denomina-se pulso e o movimento do pulso constituí uma onda. A mão da pessoa é a fonte e a corda é o meio em que a onda se propaga.

Observe na figura uma onda periódica propagando-se numa corda.

a) Classifique o tipo de onda, dizendo se é transversal ou longitudinal.


b) O que representam as distâncias a e λ.


c) Quais os nomes que são dados aos pontos A e B? E aos pontos C e D?

Resolução:

a) Como a direção de propagação é perpendicular à direção de vibração, concluímos que a onda é transversal.

b) a: amplitude; λ: comprimento de onda
c) A e B: cristas; C e D: vales

04. Observe uma onda periódica propagando-se em uma mola. Classifique o tipo de onda, dizendo se é transversal ou longitudinal.

Resolução:

Como a direção de propagação coincide com a direção de vibração, concluímos que a onda é longitudinal.

05. A vibração de uma fonte produz, em 5 segundos, ondas em uma corda que apresenta o aspecto indicado na figura. Determine:

a) a frequência

b) o comprimento de onda

c) a velocidade de propagação.

Resolução:

a) Por regra de três, temos: Em 5 s  =>  1,5 vibração. Logo em 1 s  =>  0,3 vibração. Portanto, a freqüência é f = 0,3 Hz

b) λ = 4x1cm  =>  λ = 4 cm

c) v = λ . f  =>  v = 4 . 0,3  =>  v = 1,2 cm/s

Fonte:http://www.brasilescola.com

Álvaro Gabriel Nogueira de Sousa

Categories: